미적분 주제탐구 수학 교사가 꿈인 고3인데요, 미적분 주제탐구 주제 추천해주세요
안녕하세요. 수학 교사를 꿈꾸는 고3이시군요. 미적분 주제탐구는 진로를 구체화하는 데 큰 도움이 될 겁니다. 수학 교사에게 필요한 자질과 연결될 수 있는, 흥미로우면서도 깊이 있는 주제들을 추천해 드릴게요.
1. 수학 교육과 관련된 주제
수학 교사의 핵심은 '어려운 내용을 어떻게 하면 쉽게 가르칠까'에 있습니다. 미적분을 단순히 계산하는 것을 넘어, 교육적인 측면에서 접근하는 주제는 탐구 보고서의 가치를 높일 수 있습니다.
미적분 개념의 역사적 발달과 교육적 적용 방안: 뉴턴과 라이프니츠의 미적분 발견 과정을 조사하고, 미적분 개념이 어떻게 발전해 왔는지 탐구해 보세요. 이를 바탕으로 '극한-미분-적분'의 순서가 아닌, 다른 역사적 순서로 미적분을 가르치는 새로운 교육 방법을 제안하는 보고서를 작성할 수 있습니다.
미적분학 난이도가 한국 학생들에게 어려운 이유 분석 및 해결 방안: 한국 학생들이 미적분에서 특히 어려워하는 부분이 무엇인지(예: 극한의 엄밀성, 미분 가능성 등) 통계 자료나 선행 연구를 통해 분석해 보세요. 이후 학생들이 수학적 개념을 직관적으로 이해할 수 있도록 돕는 시각화 자료(지오지브라, 데스모스 등) 활용법을 제시하는 것도 좋은 탐구 주제입니다.
2. 미적분과 타 학문 간의 융합 주제
수학 교사는 학생들에게 수학이 실생활이나 다른 학문과 어떻게 연결되는지 보여줄 수 있어야 합니다. 미적분은 다양한 분야에 응용되므로, 여러 학문과 연결된 주제를 탐구해 보세요.
미적분을 이용한 질병 확산 모델링: 감염병 확산 모델(SIR 모델 등)에 미분 방정식을 적용하여 특정 질병이 어떻게 퍼져나가는지 예측하는 과정을 탐구해 보세요. 그래프를 이용해 감염 속도, 회복 속도 등의 변화율을 시각적으로 보여주고, 이를 통해 미분과 적분의 개념을 설명할 수 있습니다.
미적분 원리를 이용한 인공지능(AI) 학습 과정 분석: AI의 핵심 기술인 딥러닝(Deep Learning)은 미분과 적분 원리를 기반으로 합니다. '경사 하강법(Gradient Descent)'과 '역전파(Backpropagation)'에 사용되는 미분 개념을 조사하고, 이를 통해 AI가 어떻게 스스로 학습하고 정확도를 높이는지 설명하는 보고서를 작성할 수 있습니다.
3. 심화 수학적 사고가 필요한 주제
수학 교사에게는 학생들의 질문에 답할 수 있는 깊이 있는 수학적 지식도 필요합니다. 교과서 수준을 넘어, 미적분 개념을 심화 탐구하는 주제는 수학적 역량을 보여줄 수 있습니다.
푸리에 급수(Fourier Series)의 원리 탐구: 복잡한 파동 함수를 단순한 삼각함수의 합으로 표현하는 푸리에 급수는 미적분의 심화 개념입니다. 음성 인식이나 이미지 처리 등 공학 분야에 널리 쓰이는 푸리에 급수의 기본 원리를 미분과 적분을 이용해 탐구해 보세요.
수학적 귀납법을 이용한 미적분 공식 증명: 교과서에 나오는 미적분 공식들을 수학적 귀납법을 이용해 증명하는 과정을 탐구해 보세요. 이는 논리적 사고력을 보여주는 좋은 방법이며, 수능 문제 해결에도 도움이 될 수 있습니다.
이러한 주제들은 단순히 지식을 나열하는 것을 넘어, 자신이 왜 수학 교사가 되고 싶은지, 어떤 교사가 되고 싶은지에 대한 고민을 담아낼 수 있습니다.
탐구 주제를 정하셨다면, 관련 논문이나 서적을 찾아보며 내용을 구체화하고, 탐구 과정과 결과를 논리적으로 정리해 보세요. 좋은 결과 있기를 응원합니다!
-
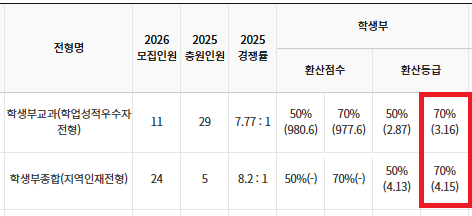
창원대 수시 .. 창원대를 목표로 하고 있는 09년생입니다 지금 제 내신이 5등급제 기준으로
2025.12.01 -

아이폰 16, 16프로 케이스 호환 가능한가요? 16을 쓰고 있는데 일반형은 케이스가 많이 없고 프로형은 많아서
2025.12.01 -

임영웅 11월 브랜드평판 순위 알고싶어요 임영웅 11월 브랜드평판에서 스타부문에서의 임영웅 순위 알고싶어요
2025.11.30 -

전주 고등학교 다자녀 제가 2027학년도 고등학교 입학생인데요 지망하는 학교가 전주 한일고인데 1. 다자녀
2025.11.30 -
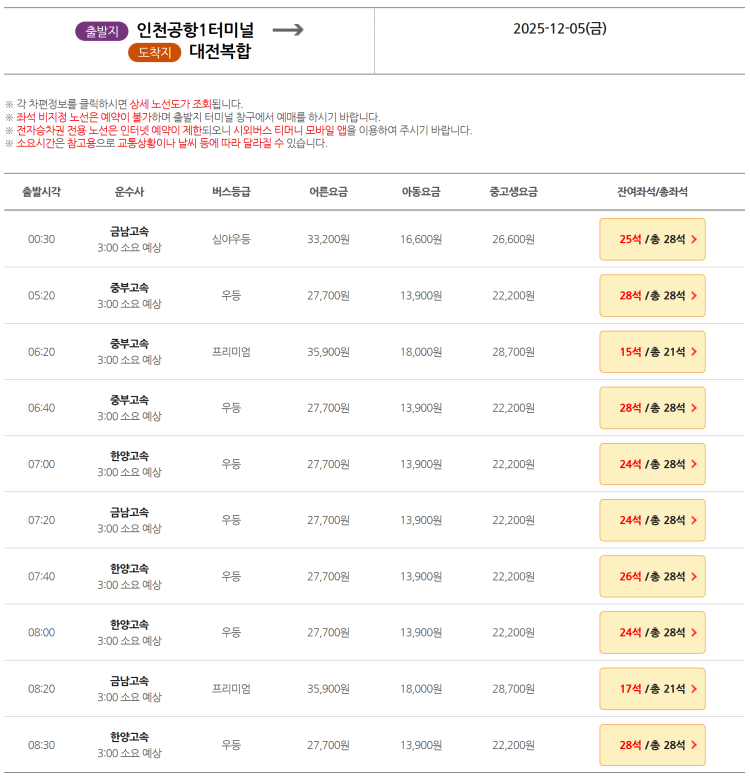
고속버스 예매 인천공항에서 대전으로 가는 버스를 이용하려하는데 버스 노선이 인천공항 2터미널에서 출발해
2025.11.30 -

어떤 야구선수 싸인일까요? 제가 옛날에 롯데 자이언츠 선수한테 싸인받은 싸인볼을 오늘 찾았네요. 어떤
2025.11.29
